Variables

Variables are Named Storage Locations for the Data / “State” of a Program

In this lesson you will learn about variables. As it turns out, you have already seen one special kind of variable, a function parameter, but we have thus far approached parameters in a way that treats them more like constants within a function definition rather than variables whose stored values can be changed, or mutated.

First, let’s start with what we know: parameters and arguments. These give us a conceptual model for introducing variables. Consider a simple function, as follows:

def f(x: int) -> int:
   return x * 2

Here, we see the declaration of a parameter named x whose type is int. In example calls to this function, using a keyword argument, we can see how an argument value is assigned to the parameter in the function call context:

print(f(x=2))
print(f(x=1 + 1))
print(f(x=f(1)))

There is an important, fundamental connection between a function call’s argument and a function definition’s parameter: in a function call, the argument value is an expression which must evaluate to the same type as the parameter’s declaration. Then, in establishing the stack frame to evaluate the function call, the argument value is assigned or “bound” to the parameter name in the context of the function call.

Let’s make this concrete with a quick example and corresponding memory diagram:

def f(x: int) -> int:
   return x * 2

print(f(x=5))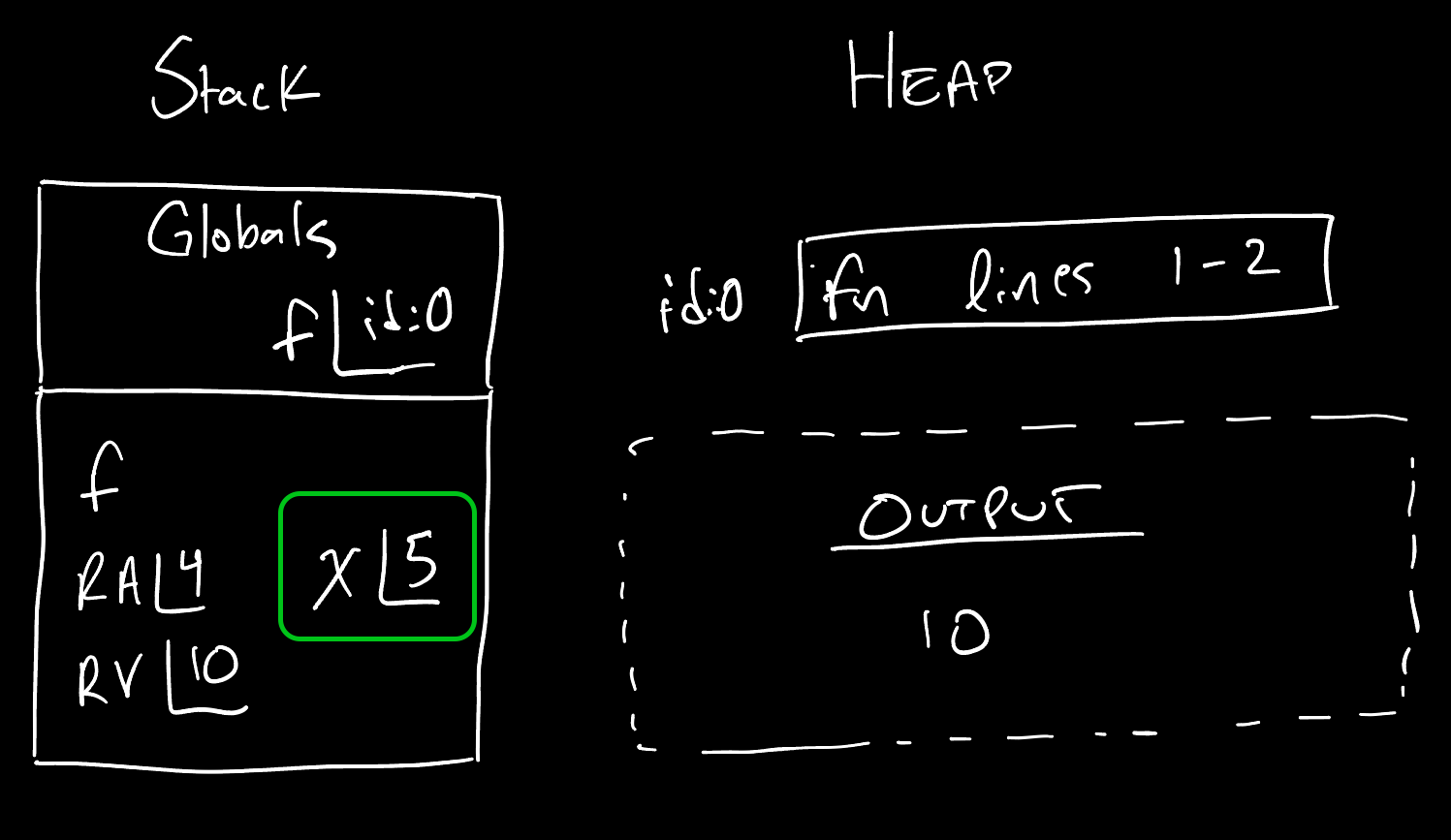

Notice the function call’s argument, 5, is bound to the parameter x in the frame evaluating the call. The important impact this has is in this frame of execution, whenever the identifier x is used, such as in the return statement’s expression x * 2, we use name resolution rules to lookup or access x’s value to understand that it is bound to a value of 5.

If multiple function calls were made in a program to the function f, then multiple frames would be evaluated on the stack each with its own value for x.

Introducing Variables

A variable is an identifier or name bound to a value held in memory.

A parameter is a special kind of variable. What makes it special are the argument assignment steps you now know and were reviewed above. Great news, though, it turns out this is much more nuanced than plain-old variables! Let’s take a look.

Variable Declaration and Initialization

Variable declaration syntax echoes parameter declaration syntax thanks to their deep relationship:

def double(x: int) -> str:
   """A silly function that doubles its argument."""
   y: int
   y = x * 2
   print(f"double({x}) is {y}")
   return y

print(double(x=3 * 2))

Notice the variable declaration statement y: int and how similarly it reads to the parameter declaration x: int. The primary difference between a variable declaration and a parameter declaration is the context in which it is defined. Parameter declarations are found in the parameter list of a function signature, whereas variable declarations are found inside of function bodies (and we will learn another place, as well).

The semantics of a variable declaration, when evaluated, are that some space in memory is reserved to hold a value and later be referenced by the name, or identifier, declared.

The following line, y = x * 2 is an example of a variable assignment statement. Notice, this echoes the keyword arguments of x=3 * 2. In both, the right-hand side is an expression that must evaluate and then be assigned or bound to the variable on the left-hand side variable or paramter, respectively.

Let’s diagram the above code listing for illustration purposes:

Notice the declaration of y leads to a new entry for y in the stack frame for a call to double. Following the evaluation of y: int this entry would be empty, however, the following variable assignment statement y = x * 2 initializes the variable y to the evaluation of x * 2, which in this frame of execution, because x is assigned 6, y is assigned 12.

Combined Declaration and Initialization

You will commonly want to declare and immediately initialize a variable following declaration. While this was broken down into two sequential steps above to introduce these independent concepts, they are more often combined:

def double(x: int) -> str:
   """A silly function that doubles its argument."""
   y: int = x * 2
   print(f"double({x}) is {y}")
   return y

print(double(x=3 * 2))

Order of Initialization and Access Matters

Consider the following erroneous function:

def f() -> int:
   x: int
   print(x)
   x = 1
   print(x)
   return x

Here, we attempted to access x before it was initialized. If you were to write and call this function you would see the following error:

UnboundLocalError: cannot access local variable 'x' where it is not associated with a value

Read the error closely. These are terms you know: “access” (use/read), “local” (inside of a function body), “variable”, “associated with a value” (assignment)! An UnboundLocalError occurs when you attempt to access a variable declared in a function before it is initialized.

Similarly, if you attempt to reference a variable that has no declaration statement, you will see a NameError:

def f() -> int:
   x0: int = 1
   print(x_0)
   return x_0

Evaluating this function f will result in:

NameError: name 'x_0' is not defined. Did you mean: 'x0'?

Notice, Python is attempting to be very helpful here and sees the variable name you attempted to print and return is close to another variable name declared and initialized. Perhaps it was an accidental typo or a renaming of a variable that missed accesses anywhere: these are both common occurances in programming. In any case, a NameError occurs when accessing a variable, or identifier more precisely, that has not been defined.

Terminology

There are four important pieces of terminology to know here:

1. Variable Declaration: Defines and establishes a variable name and its data type.
2. Variable Assignment Statement: A statement whose left-hand side is a variable name and right hand side is an expression that, after full evaluation, is the value bound to the variable name in memory. This value’s type must be in agreement with the variable’s declared type for a well-typed program.
3. Variable Initialization: The special name given to a variable’s first assignment. You must always initialize a variable before accessing or reading from it.
4. Variable Access: The usage of a variable’s identifier in an expression. When evaluated, name resolution rules will lookup the value the identifer is bound to in memory and substitute its current value.

Why variables? 1. Storage of computed values and input data.

Variables are named locations in memory to store data. They give you the ability to store, or asssign, the result of a computed value, or value input by a user, or data loaded from an external source source. Once assigned, a variable can be accessed later in your program without the need to redo the computation, ask the user again, or reload data. One common use for this is breaking a complex expression down into simpler steps. For example, compare the following two function definitions:

def distance(a: tuple[float, float], b: tuple[float, float]) -> float:
   """Distance between two points."""
   return ((b[0] - a[0]) ** 2.0 + (b[1] - a[1]) ** 2.0) ** 0.5

This compound expression could be broken down into simpler pieces with intermediate values stored in variables:

def distance(a: tuple[float, float], b: tuple[float, float]) -> float:
   """Distance between two points."""
   x_delta: float = (b[0] - a[0]) ** 2.0
   y_delta: float = (b[1] - a[1]) ** 2.0
   return (x_delta + y_delta) ** 0.5

Additionally, consider the following example which asks the user for input and reuses the input multiple times over:

def main() -> None:
   an_int: int = int(input("Provide a number: "))

   if an_int % 2 == 0:
      print(f"{an_int} is even")
   else:
      print(f"{an_int} is odd")

   if an_int == 0:
      print(f"{an_int} is zero")
   elif an_int > 0:
      print(f"{an_int} is positive")
   else:
      print(f"{an_int} is negative")

if __name__ == "__main__":
   main()

Notice the variable an_int is accessed in many different expressions following. If you were not able to store the user input in memory by binding the input value to a variable, you would need to ask the user for input many times over. This would be frustrating!

Why Variables? 2. The ability to update “state” in memory

Named constants are quite similar to variables, but there is a key difference: constants intend to stay constant whereas variables are able to vary, “change value”, or be reassigned.

This feature of variables requires you to unlearn some expectations you learned in algebra about variables in an algebraic sense. Let’s take a look at an exampe:

def increment(x: int) -> int:
   y: int = x
   y = y + 1
   print(f"x: {x}, y: {y}")
   return y

print(increment(x=1))

Before continuing on, try reading this example and predicting its outputs without tracing in a memory diagram. Then, try tracing in a memory diagram. Finally, try comparing your memory diagram to below and checking to see if your intuitions were correct. It is OK if your intuition is not correct here! In fact, it is quite common! This breaks a mental model from mathematics and the memory diagram can help us understand why:

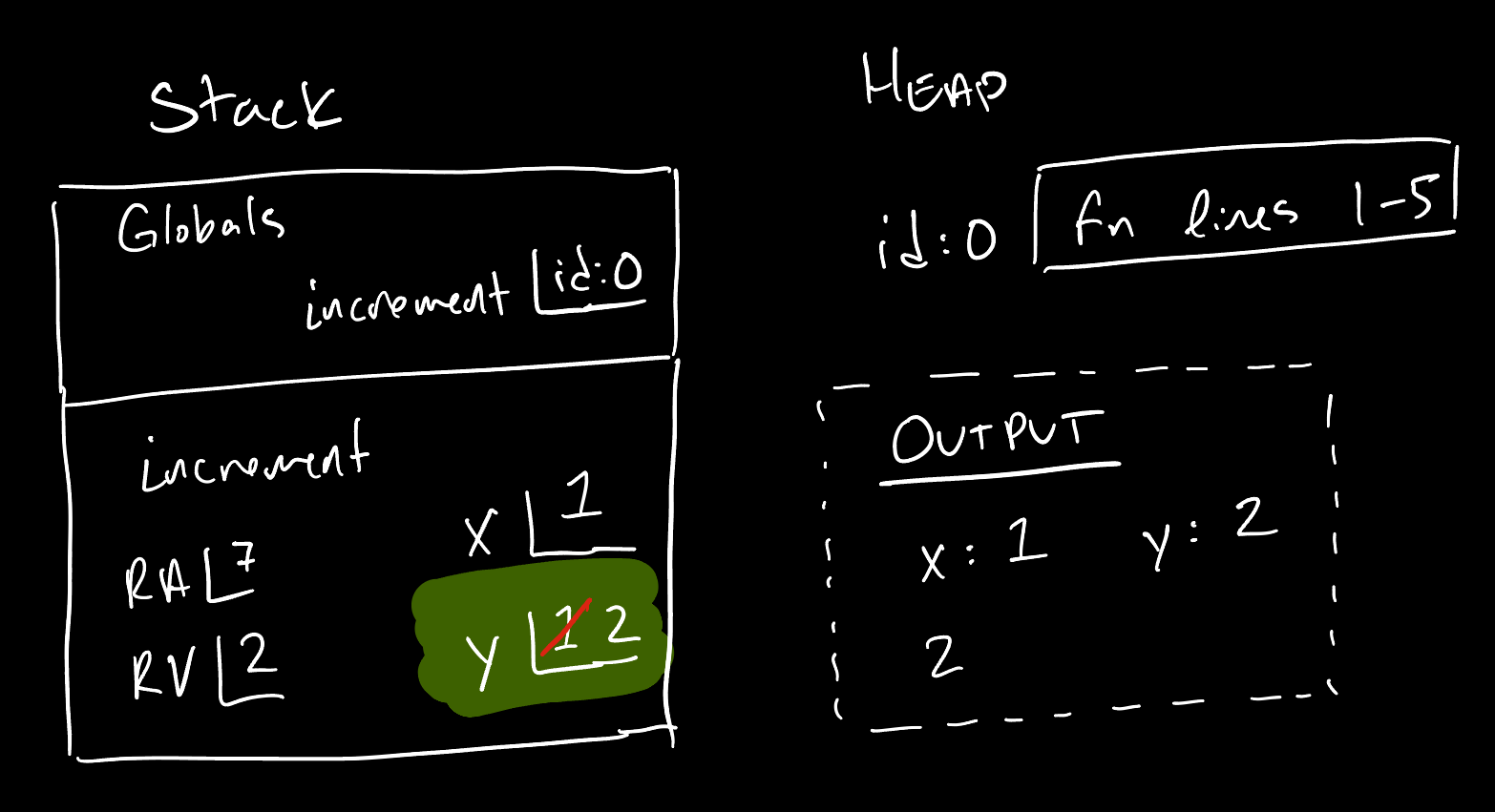
Let’s break down the important lines:

1. y: int = x - Variable y is declared and initialized to be the current value of x. The right-hand side expression x uses name resolution to lookup x in the current frame of execution to see it is bound to 1. Thus, y is initialized to a value of 1.
2. y = y + 1 - This kind of variable assignment statement, where the same variable name is used on both sides of the assignment operator, is the most surprising to first time programers on first glance! But you know how to break this down and recognize there is an important difference in meaning of the y on each side. It helps to read assignment statements in English: “y is assigned y’s current value plus 1.” Try to develop a habit of reading the assignment operator, which is =, as “is assigned” or “takes the value of” or “is bound to” or “is associated with” and try your best not to read it as “is equal to.”

Remember, in an assignment statement like y = y + 1, always focus your attention to the right hand side of the assignment operator = first. This is an expression. It must evaluate to a value of the same type as the variable’s declaration. In this case, the expression is y + 1 which contains a variable access to y which is originally bound to a value of 1. Then, 1 + 1 evaluates to 2. Once the right-hand side evaluation completes, the value is then bound to the variable whose name is in the left-hand side, y, in the current frame of execution.

Important common misconception: using a variable in an expression which assigns to another variable does not create a relationship between variables, it merely copies the value it is bound to.

Notice in this example, where y: int = x, we did not write x into the stack frame. This is thanks to the evaluation rules described above: we lookup the value x is currently bound, which was 1, to and then bind this value to y, as well. Therefore, when we later reassign a new value to y it has no impact on x. The same would be true, vice-versa, if we had reassigned a new value to x.

In our memory diagrams, we cross out the existing value of a variable and write-in the newly assigned value. This gives us “proof of work” to understand how memory was updated. In reality, though, when a variable is reassigned, its old value is “clobbered” or fully replaced by the new value. When a variable is reassigned to be a new value, there is no retrieving the old value without recomputing it, somehow, or storing it in another variable as a “backup.”

Big idea: notice in reassigning a new value to a variable does not require new space in memory. We will come back to this feature soon.

Intoducing while Loop Statements

Now that you understand what a variable is, it is time to learn a powerful new kind of statement: a while loop statement.

A while statement, like an if statement, is related to the control flow of a program. Control flow refers to where “control” or the next line of execution continues to next. Like an if statement, it has a boolean expression test condition and a body. Unlike an if statement, when control finishes with the last line of the body, it jumps or loops back up to the boolean test expression again. Let’s take a look:

def print_0_to_n(n: int) -> int:
   counter: int = 0
   while counter < n:
      print(counter)
      counter = counter + 1

   print(f"Final: {counter}")
   return counter

print(print_0_to_n(n=4))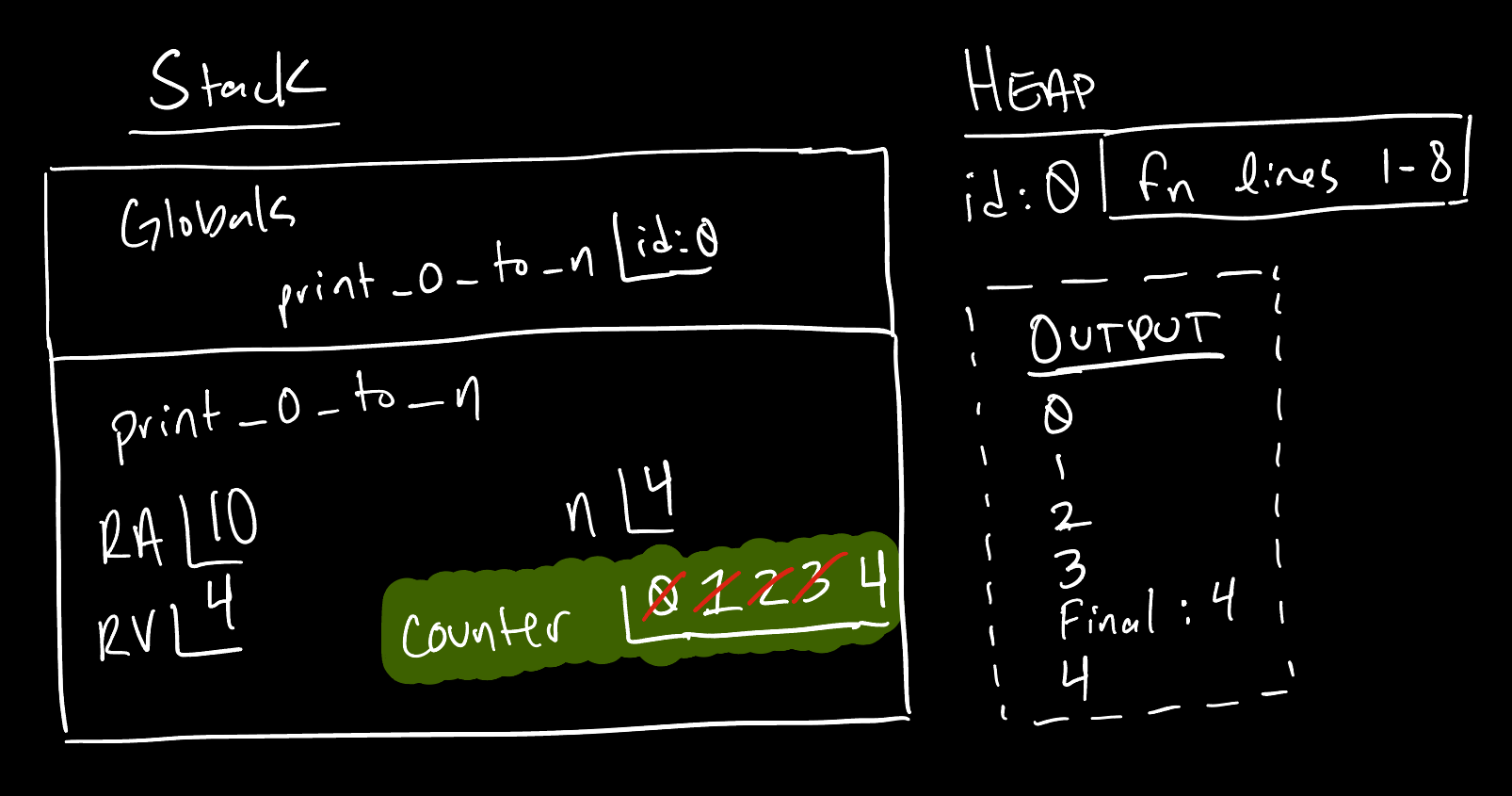

Notice with a while loop, we are able to achieve repeating pattern similar to how we did with recursion, but with using only a single function call frame. This is possible thanks to the combination of the counter variable’s value being incremented by one each time the while body reaches the line counter = counter + 1, before jumping back to the test of counter < n and repeating anew. Eventually, counter’s value is incremented to no longer be less than n and the loop completes. Control then jumps to the next line following the loop body, the print statement, and finally returns the current value of counter.

Iterating over a Sequence

Looping is more precisely called iteration when some value “iterates”, or makes small steps of progress, toward some goal. In the previous example, the counter variable iterated toward n.

Another use of iteration is iterating through the indices of a sequence. Recall tuples and strs are sequences with ordered items addressed by a 0-based index using subscription, sequence[index], notation. Let’s try reversing a string by iterating through each of its characters and using concatenation:

def reverse(a_str: str) -> str:
   """Reverse a string"""
   idx: int = 0
   result: str = ""
   while idx < len(a_str):
      result = a_str[idx] + result
      idx = idx + 1
   
   return result

print(reverse("abc"))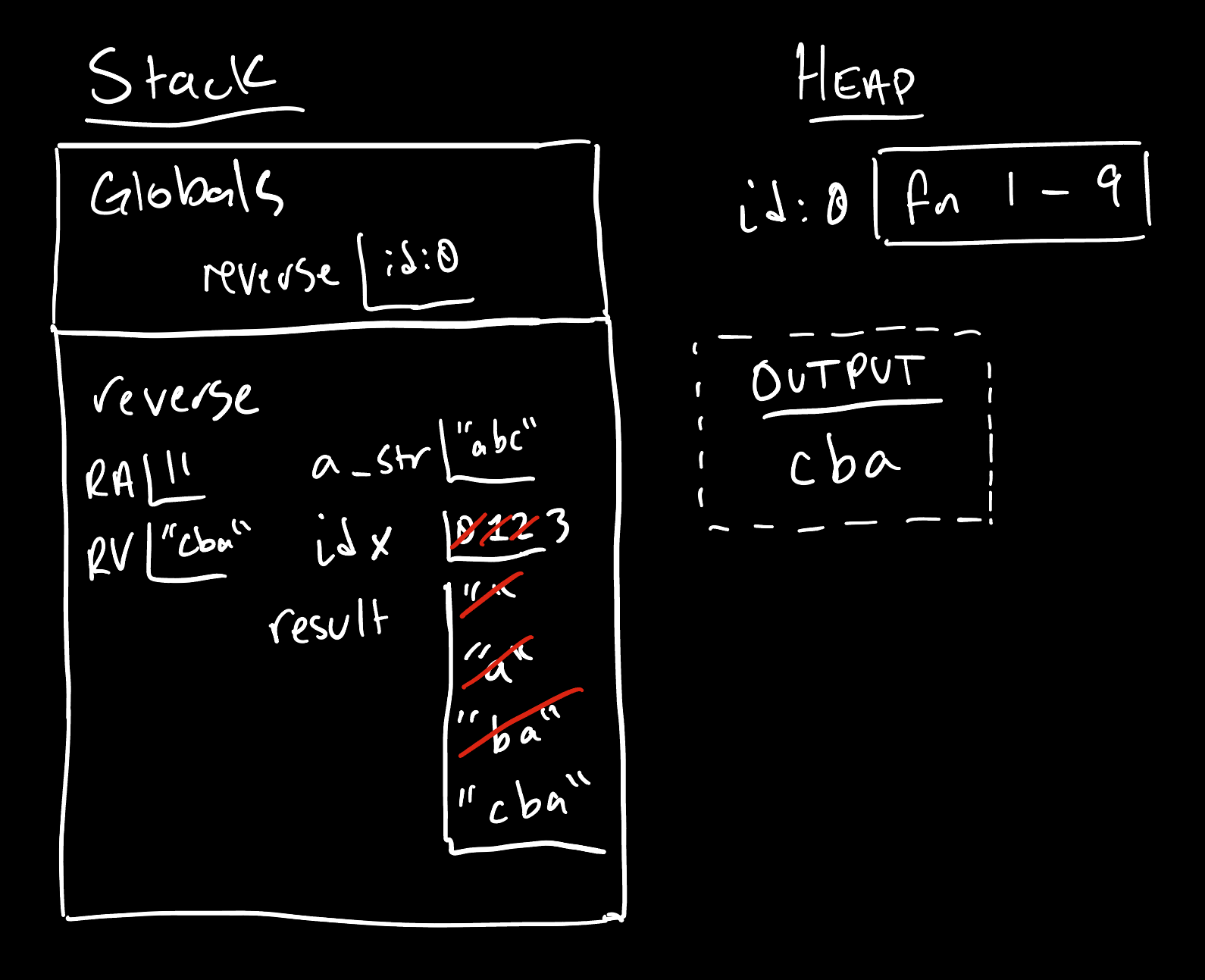

Notice how these variables are declared ahead of the loops and each serves a unique purpose. The idx variable keeps track of the index at which the iterative process is working on. The result variable keeps track of the “work in progress” result and updates it in the process of each iteration. Inside the loop body, importantly, the idx variable is increasing and iterating its way toward being at least len(a_str), which is the loop’s exit condition.

Big Iterative Idea: Space Efficient

In contrast to the recursive algorithms that accumulated a value through recursive function calls where each call needed more space in memory on the call stack, with variable reassignment and loops we can write algorithms that make a more efficient use of space. There are no free lunches, though! Writing algorithms using these iterative techniques is generally more error prone and requires even more care and consideration to be done correctly. We will be looking strategies for writing correct looping algorithms next.